Pole koła to miara powierzchni ograniczonej przez okrąg. Jest to jedna z najważniejszych wielkości geometrycznych, która ma wiele zastosowań w matematyce, fizyce, inżynierii i innych dziedzinach. W tym artykule przedstawimy kilka sposobów obliczania pola koła i jego części, czyli wycinka koła.
Jak obliczyć pole koła mając średnicę
Średnica koła to odcinek łączący dwa punkty na okręgu i przechodzący przez środek koła. Długość średnicy oznaczamy zazwyczaj przez **d**. Aby obliczyć pole koła mając średnicę, wystarczy zastosować następujący wzór:
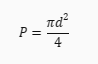
Gdzie **P** to pole koła, a **π** to stała matematyczna o przybliżonej wartości **3,14**.
Oblicz ile w przybliżeniu wynosi pole koła
Aby obliczyć ile w przybliżeniu wynosi pole koła, możemy skorzystać z powyższego wzoru i podstawić dowolną wartość średnicy. Na przykład, jeśli średnica koła wynosi **10 cm**, to pole koła wynosi:
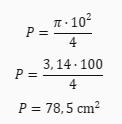
Możesz poćwiczyć z dzieckiem obliczenia pola koła, korzystając z gotowych zadaniach dla dzieci do druku. Znajdziesz tam zadania z matematyki i innych przedmiotów ścisłych.
Jaki jest wzór na pole koła
Wzór na pole koła można wyprowadzić na kilka sposobów. Jednym z nich jest wykorzystanie faktu, że pole koła jest równe iloczynowi długości promienia i długości łuku okręgu. Promień koła to odcinek łączący środek koła z dowolnym punktem na okręgu. Długość promienia oznaczamy zazwyczaj przez **r**. Długość łuku okręgu to część obwodu koła odpowiadająca danemu kątowi środkowemu. Długość łuku okręgu oznaczamy przez **l**. Kąt środkowy to kąt między dwoma promieniami wychodzącymi ze środka koła. Kąt środkowy oznaczamy przez **α**. Zależność między długością łuku okręgu a kątem środkowym jest następująca:
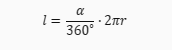
Gdzie **360°** to miara pełnego kąta, a **2πr** to obwód koła.
Jeśli chcemy obliczyć pole całego koła, musimy wziąć pod uwagę wszystkie możliwe kąty środkowe i odpowiadające im łuki okręgu. Zauważmy, że suma wszystkich kątów środkowych jest równa **360°**, a suma wszystkich łuków okręgu jest równa obwodowi koła. Zatem pole całego koła jest równe iloczynowi promienia i obwodu koła:
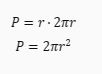
Jeśli podzielimy obie strony równania przez **2**, otrzymamy inny wzór na pole koła:
![]()
Ten wzór jest równoważny poprzedniemu i często jest używany do obliczania pola koła.
Jak obliczyć pole powierzchni koła
Pole powierzchni koła to pojęcie używane w geometrii przestrzennej do określenia powierzchni ograniczonej przez sferę. Sfera to bryła geometryczna składająca się ze wszystkich punktów w przestrzeni, które są w stałej odległości od pewnego punktu nazywanego środkiem sfery. Odległość ta nazywa się promieniem sfery i oznacza się ją tak samo jak promień koła, czyli przez **r**. Aby obliczyć pole powierzchni koła, wystarczy zastosować następujący wzór:
![]()
Gdzie **S** to pole powierzchni koła, a **π** to stała matematyczna o przybliżonej wartości **3,14**.
Jak się liczy pole koła
Pole koła można liczyć na kilka sposobów, w zależności od tego, jakie dane mamy podane. Najczęściej używane są dwa wzory:
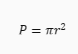
Gdzie **P** to pole koła, **r** to promień koła, a **π** to stała matematyczna o przybliżonej wartości **3,14**.
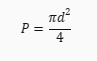
Gdzie **P** to pole koła, **d** to średnica koła, a **π** to stała matematyczna o przybliżonej wartości **3,14**.
Aby skorzystać z tych wzorów, musimy znać albo promień, albo średnicę koła. Jeśli znamy tylko obwód koła, możemy go wykorzystać do obliczenia promienia lub średnicy. Obwód koła to długość linii ograniczającej koło. Obwód koła oznaczamy przez **C**. Zależność między obwodem a promieniem lub średnicą jest następująca:
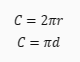
Gdzie **C** to obwód koła, **r** to promień koła, **d** to średnica koła, a **π** to stała matematyczna o przybliżonej wartości **3,14**.
Jeśli znamy tylko obwód koła, możemy go podzielić przez **π**, aby otrzymać średnicę, lub podzielić przez **2π**, aby otrzymać promień. Następnie możemy podstawić te wartości do wzorów na pole koła.
Jak obliczyć pole wycinka koła
Wycinek koła to część powierzchni koła ograniczona przez dwa promienie i łuk okręgu. Wycinek koła ma kształt podobny do kawałka ciasta lub pizzy. Aby obliczyć pole wycinka koła, musimy znać kąt środkowy odpowiadający temu wycinkowi oraz promień koła. Kąt środkowy to kąt między dwoma promieniami wychodzącymi ze środka koła. Kąt środkowy oznaczamy przez **α**. Promień koła to odcinek łączący środek koła z dowolnym punktem na okręgu. Promień koła oznaczamy przez **r**. Wzór na pole wycinka koła jest następujący:
![]()
Gdzie **P_w** to pole wycinka koła, **α** to kąt środkowy w stopniach, **r** to promień koła, a **π** to stała matematyczna o przybliżonej wartości **3,14**.
Ten wzór wynika z faktu, że stosunek pola wycinka do pola całego koła jest równy stosunkowi kąta środkowego do pełnego kąta. Innymi słowy:
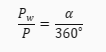
O ile procent pole koła opisanego na trójkącie równobocznym jest większe od pola koła
Trójkąt równoboczny to taki trójkąt, który ma wszystkie boki równe i wszystkie kąty równe 60 stopni. Koło opisane na trójkącie równobocznym ma środek w punkcie przecięcia się wysokości trójkąta. Wysokość trójkąta równobocznego jest równa połowie długości boku pomnożonej przez pierwiastek z 3. Promień okręgu opisanego na trójkącie równobocznym jest równy połowie długości boku pomnożonej przez pierwiastek z 3 podzielonym przez 2. Aby obliczyć o ile procent pole koła opisanego na trójkącie równobocznym jest większe od pola tego trójkąta, musimy znać długość boku trójkąta i jego pole. Długość boku trójkąta oznaczamy przez **a**, a pole trójkąta przez **S**. Wzór na o ile procent pole koła opisanego na trójkącie równobocznym jest większe od pola tego trójkąta jest następujący:
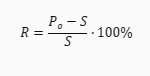
Gdzie **R** to wzrost pola wyrażony w procentach, **P_o** to pole koła opisanego na trójkącie równobocznym, a **S** to pole trójkąta równobocznego.
Ten wzór wynika z faktu, że stosunek wzrostu pola do pola trójkąta jest równy stosunkowi liczby procentowej do liczby 100. Innymi słowy:
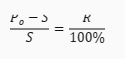
Ile razy pole koła jest większe od pola kwadratu
Kwadrat to czworokąt, który ma wszystkie boki równe i wszystkie kąty proste. Koło jest większe od kwadratu, jeśli jego średnica jest równa przekątnej kwadratu. Przekątna kwadratu jest równa długości boku pomnożonej przez pierwiastek z 2. Aby obliczyć ile razy pole koła jest większe od pola kwadratu, musimy znać długość boku kwadratu i jego pole. Długość boku kwadratu oznaczamy przez **a**, a pole kwadratu przez **S_k**. Wzór na ile razy pole koła jest większe od pola kwadratu jest następujący:
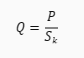
Gdzie **Q** to iloraz pola koła i pola kwadratu, **P** to pole koła, a **S_k** to pole kwadratu.
Ten wzór wynika z faktu, że stosunek pola koła do pola kwadratu jest równy stosunkowi średnicy koła do przekątnej kwadratu podniesionemu do kwadratu. Innymi słowy:
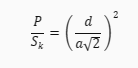
Gdzie **d** to średnica koła, a **a** to długość boku kwadratu.
Ile razy pole koła opisanego na trójkącie równobocznym jest większe od pola koła
Koło opisanego na trójkącie równobocznym jest większe od koła wpisanego w ten trójkąt. Koło wpisane w trójkąt równoboczny ma środek w punkcie przecięcia się symetralnych boków trójkąta. Symetralna boku to prosta przechodząca przez środek tego boku i prostopadła do niego. Promień okręgu wpisanego w trójkąt równoboczny jest równy połowie długości boku pomnożonej przez pierwiastek z 3 podzielonym przez 3. Aby obliczyć ile razy pole koła opisanego na trójkącie równobocznym jest większe od pola koła wpisanego w ten trójkąt, musimy znać długość boku trójkąta i jego pole. Długość boku trójkąta oznaczamy przez **a**, a pole trójkąta przez **S**. Wzór na ile razy pole koła opisanego na trójkącie równobocznym jest większe od pola koła wpisanego w ten trójkąt jest następujący:
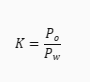
Gdzie **K** to iloraz pola koła opisanego i pola koła wpisanego, **P_o** to pole koła opisanego na trójkącie równobocznym, a **P_w** to pole koła wpisanego w trójkąt równoboczny.
To wszystko! Jeśli jednak chcesz przypomnieć sobie podstawy matematyki, możesz przeczytać także, co to jest iloczyn i jak go obliczać.






